3333 (グラフの準備:漸近線の求め方 (無理関数)) 2 3,161 ビュー 見て頂いてありがとうございます. 見てもらうために作成しておりますので,どんどん見てください. ★の数は優先度です.★→★★→★★★ の順に取り組みましょう. 3332 30 ←3332なり,中心から離れるほど2 つの漸近線(X 軸,Y 軸) に限りなく近づいていく性質を持つ。その2 つの曲線の うちの片方だけでも双曲線といい,本研究でも直角双曲 線として一般的な式(1)を,第三段階の推定式として用い ることにする。 (at b) t U = (1)漸近線とは、曲線が近づく直線のことをいい、x軸に平行な漸近線、y軸に平行な漸近線、y=mxnの形の漸近線の3種類があります。 単元 積分, キーワード 漸近線,分数関数,対数,指数,分数,双曲線,無理関数,傾き,切片,例題,解法,微分,極限,求め方,log,logarithm見て頂い

双曲線の漸近線の簡単な求め方と証明 高校数学の美しい物語
漸近線 求め方 双曲線
漸近線 求め方 双曲線-したがって,漸近線の方程式を単独で問うことはまれです。 漸近線とは,一言で言えば「ある曲線が限りなく近づく相手方の線」のことですが,高校数学で漸近線と言えば「直線」に限ります (*)。 したがって,高校数学の漸近線は (A) 縦線:「x軸に垂直双曲線の準円 双曲線の場合も様子は似ていますが,注意すべきことがいくつかあります。 計算は楕円の場合よりめんどくさい(拡大,縮小して円にするテクニックが使えない)ので結果のみ記します。 (図の赤い円が準円,軌跡としては漸近線上の四点




双曲線とは 例題と要点まとめでマスターしよう 高校生向け受験応援メディア 受験のミカタ
4 双曲線 ・双曲線の方程式,焦点の座標及び漸近線を 求め,双曲線の概形をグラフに表すことが できる。 5 二次曲線と直 ・二次曲線と直線との共有点の個数を理解し 線の共有点 ている。 6 二次曲線の ・平行移動のよさについて関心をもち,平行 例えば、 {(x1)^2}/9{(y3)^2}/16=1 という方程式で表される双曲線には、 準線が2本存在するという認識で合っていますか? (ya)^2=4*b(xc)の焦点の求め方 1901 お世話になります 楕円の方程式の場合、長いほうの半径を短いほうの半径へと三平方の定理を用いて焦点をだす方法、そして、双曲線の場合、漸近線にピークの値を代入することで同じく三平方より焦点をだすやり
10双曲線 双曲線の中心と頂点高校数学Ⅲ 双曲線の焦点と漸近線高校数学Ⅲ 双曲線の方程式高校数学Ⅲ 直角双曲線とは高校数学Ⅲ 双曲線の平行移動高校数学Ⅲ 双曲線の領域高校数学Ⅲ 11二次曲線と直線 一方、漸近線を決めた場合、双曲線の2本の漸近線を x/ay/b=0 と x/ay/b=0 とした場合は、その2本の漸近線に関して双曲線群を考えることができます。Rをパラメータとして、 (x/a)^2(y/b)^2=R^2 と (x/a)^2(y/b)^2=R^2 は2組の双曲線群を表しています。漸近展開に関するメモ 漸近展開に関するメモ Landau の記号と漸近展開 ver13 京都府立鳥羽高校定時制 稲葉芳成 はじめに この文章は, 大学初年度向けの微分積分のテキストである, 「三宅敏恒著『入門微分積分』培風館」を参考にして, 内容が平易で
漸近線である。 漸近線の求め方 y=f(x) の漸近線がy ax b とすると,x が+∞ある いは-∞のとき,y の値はほぼ同じと考えられるので, f(x)≒ax+b ・・・① とおける。両辺をx で割って,lim計算すると, lim( ) ( ) lim x b a x f x x x よって, x f x a x ( ) lim※この頁では漸近線の方程式の求め方を解説します. (1) 縦方向の( x 軸に垂直な)漸近線 有限の値 a に対して, x→a のとき y→∞ または y→−∞ になるとき, x=a が漸近線になります. 直角双曲線 a = b a = b のときは、先ほど求め双曲線の漸近線は x a − y a = 0, x a y a = 0 x a − y a = 0, x a y a = 0 となります。 これは、書き換えれば、 y = x y = x, y = −x y = − x の2つです。 これらは直交します。 このように、漸近線が直交する双曲線のことを



1
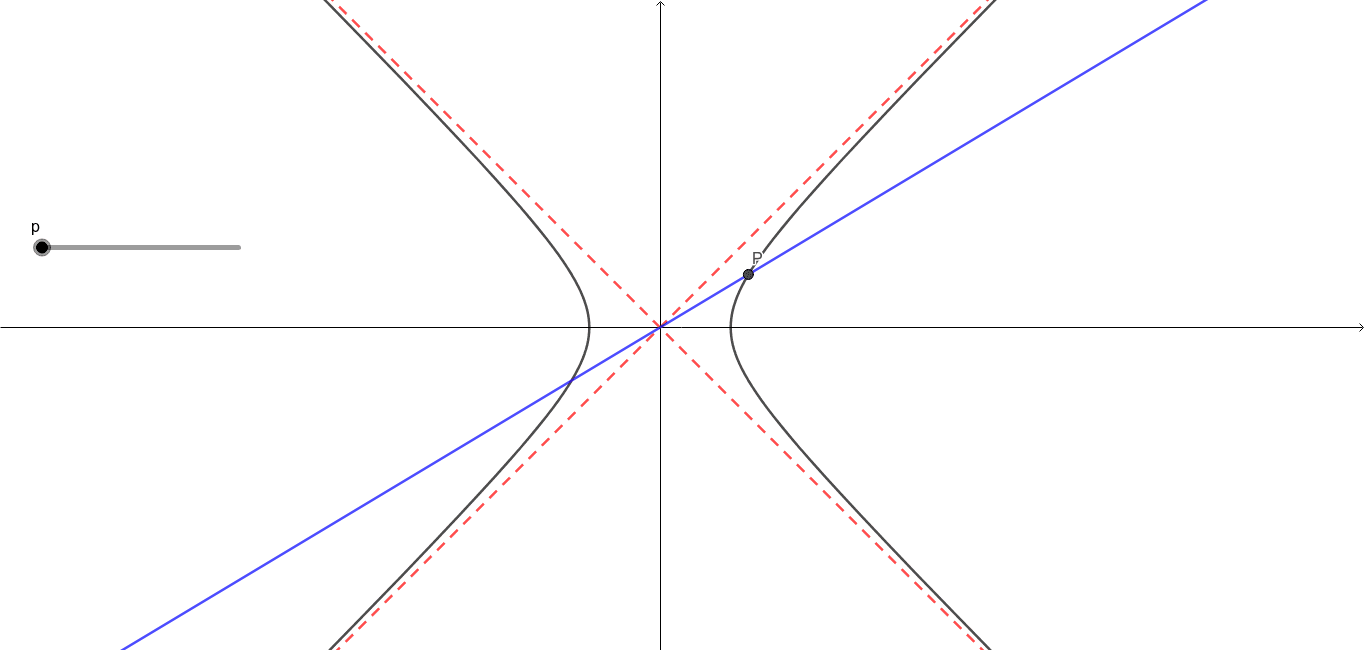



双曲線の漸近線 Geogebra
3 漸近線の求め方 31 軸に平行な漸近線の求め方 32 軸に平行でない漸近線の求め方2STEP 321 STEP1 の極限を調べる→傾きチェック 322 STEP2 代入する 4 漸近線の有無の判別方法 41 チェック① 軸に平行でない漸近線があるか 42 チェック② 不連続な点が 双曲線の概形の書き方 2341 たとえば(x2)^2 (y3)^2=1 というときx^2 y^2=1を x軸方向に2 yに3平行移動したもの。 とわかってそこが中心になるっていうことは分かります。 そこで、双曲線の頂点といったらいいのか・・・ 呼び方はわかりませんが 双曲線とは 双曲線とは、円錐を上下に2つ重ねて斜めに切ると断面に現れる二次曲線で(図1参照)、その概形は下のグラフの通りです。 <双曲線と円錐(再掲)> <双曲線のグラ




曲線 漸近線 求め方 2973 曲線 漸近線 求め方 Mbaheblogjpbmo0




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ
双曲線 近似 エクセル WordやExcelで初心者が図形(オートシェイプ)を描く練習をするときに最初につまづくのが曲線と折れ線ではないでしょうか? 直線は鉛筆で描くようにドラッグをしますが、曲線(スプライン曲線)や折れ線(フリーフォーム)をか この双曲線の漸近線は、 y = ±( b/a )x です。 双曲線の焦点の座標は、 c = √( a^2 b^2 ) として ( ±c , 0 ) です。 また、離心率 e は、 e = a / c です。 また、双曲線上の点の二つの焦点からの距離の差は、一定値 2a になります。 漸近線は、 基本双曲線と漸近線 や 基本一次分数関数のグラフ などでも出てきていますが、このページの後半で、もう少し詳しく見ることにしましょう。 基本微分と関数のグラフ を参考にしつつ考えていきましょう。 まず、増減を調べる



この双曲線の漸近線ってどうなるんですか 教えてください B Aだけど上がx Yahoo 知恵袋




1996 号 道路消失点の算出方法及び車両の位置 姿勢計測装置 Astamuse
一方、漸近線を決めた場合、双曲線の2本の漸近線を x/ay/b=0 と x/ay/b=0 とした場合は、その2本の漸近線に関して双曲線群を考えることができます。Rをパラメータとして、 (x/a)^2(y/b)^2=R^2 と (x/a)^2(y/b)^2=R^2 は2組の双曲線群を表しています。ここで x 2 (x') 2 が消えてほしいのですが、消えません。 うまく消すためには右辺の x 2 (x') 2 の前が にならないといけません。 そのためには、その前の右辺の x 2 の前に負号をつけるか、 (x') 2 の前の負号を にするかですが、前者は双曲線の方程式から来ていて譲れませんから、後者、つまり こんにちは。 da Vinch (@mathsouko_vinch)です。この記事のトピックは「双曲線の方程式の導出とグラフの書き方」です。 双曲線を軌跡で考える二次曲線はいろいろな条件の軌跡を考えることでその概形が決まります。今回は「双




Pから双曲線にひいた2つの接線が直交するときの軌跡 双曲線の準円 数学の偏差値を上げて合格を目指す



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典
双曲線 式 双曲線 (そうきょくせん、 英 hyperbola )とは、2次元 ユークリッド空間 R2 上で定義され、ある2点 P, Q からの 距離 の「差が一定」であるような 曲線 の総称である。 この P, Q は 焦点 と呼ばれる 双曲線には、図にも書いていますが漸近線 (読み うさぎでもわかる線形代数 第21羽 2次形式の応用・2次曲線のグラフ 19年9月6日 19年9月6日 36分52秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は、前回まとめた2次形式の標準形の変換を応用して、2次曲線のグラフを書いてみる方法数学・算数 2次曲線 双曲線 X²-Y²/9=1→(x²-9分のY²=1) の焦点と漸近線の方程式の求め方、さらにP1(2、3√3)における接戦の方程式の求め方をおしえてください。 質問No




数 の二次曲線についてです Clearnote



双曲線の方程式
漸近線の求め方を解説しました。 グラフの漸近線は、x軸に垂直な漸近線とそうでない漸近線とがあります。 そうでない漸近線は、\(x\to\pm\infty\)において漸近線と曲線が限りなく近づきます。 漸近線の方程式を\(y=axb\)とすると、曲線\(y=f(x)\)の漸近線は、②2つの焦点がy軸上にある双曲線 (x 2 /a 2)(y 2 /b 2)=1 のグラフの描き方はわかりましたね。a,bの値を求め,頂点の座標と漸近線から双曲線を描けばよいのです。仕上げに,焦点の座標の求め方を確認しておきましょう。双曲線関数でおいて解くことにします.特に (2)は x √ x 2 − 1 = t x x 2 − 1 = t とおく置換が楽です. 以下 C C を積分定数とする. (1) x = e θ − e − θ 2 = sinh θ x = e θ − e − θ 2 = sinh θ , d x = e θ e − θ 2 d θ = cosh θ d θ d x = e θ e − θ 2 d θ = cosh θ




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
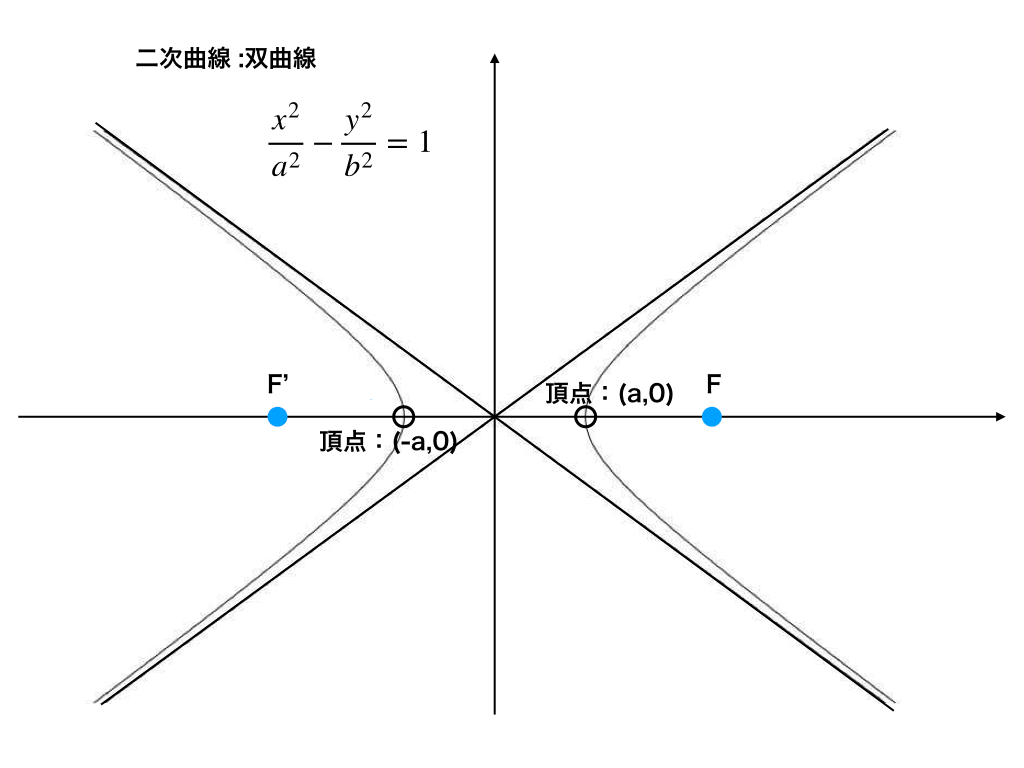



曲線 漸近線 求め方 2973 曲線 漸近線 求め方 Mbaheblogjpbmo0
アポロニウスは、ユークリッドの後の人で、アルキメデスとほぼ同時代。 bc225年頃に円錐曲線論8巻を著した。 この著は、ルネッサンスの「科学者」ガリレオ、ケプラーたちの自然探究に多大な影響を与える。 そして、射影幾何学へと発展する。例えば曲線 y = x2 1xn は x→±∞において y = x2 に限りなく近づきますが,高校では漸近線として y = x2 を求める必要はありません。この例では, 縦線: x = 0 だけが漸近線です。 (A) 「縦」の漸近線の求め方 有限の値 a に対して, limx→a 単元 積分, 「漸近線の描き方を一目にまとめました。 漸近線とは、曲線が近づく直線のことをいい、x軸に平行な漸近線、y軸に平行な漸近線、y=mxnの形の漸近線の3種類があります。」, キーワード 漸近線,分数関数,対数,指数,分数,双曲線,無理関数,傾き,切片,例題,解法,微分,極限,求め方




双曲線とは 例題と要点まとめでマスターしよう 高校生向け受験応援メディア 受験のミカタ




双曲線の漸近線の簡単な求め方と証明 高校数学の美しい物語
②2つの焦点がy軸上にある双曲線 (x 2 /a 2)(y 2 /b 2)=1 のグラフの描き方はわかりましたね。a,bの値を求め,頂点の座標と漸近線から双曲線を描けばよいのです。仕上げに,焦点の座標の求め方を確認しておきましょう。 1 1 回答 2点 (2a 2 a は双曲線の x x 軸との交点の距離の差である. 2a =a−(−a) 2 a = a − ( − a) より,双曲線の x x 軸との交点の x x 座標の値は a a , −a − a である. この双曲線を表す 方程式 は x2 a2 − y2 b2 =1 x 2 a 2 − y 2 b 2 = 1 (ただし, b= √c2−a2 b = c 2 − a 2 ) となるただ、近似曲線を表示したものの式が出ていないことがあります。 ここでは、近似曲線の計算式を表示させたり、近似曲線から値を求める方法について解説していきます。 ・近似曲線を表示させる方法の式を出す方法 ・近似曲線の数式から値を求める方法




漸近線の描き方 一目瞭然早見チャート 高校生 数学のノート Clearnote




漸近線 Wikipedia
この問題は、双曲線のグラフをかくことが目的の問題ではないので、大まかな形がわかればいいのです。 頂点と漸近線を求めれば簡単にグラフはかけますよ。 そこで、 という手順で考えてみましょう。 すると、右図の青線で表された双曲線のグラフが



1



双曲線の方程式
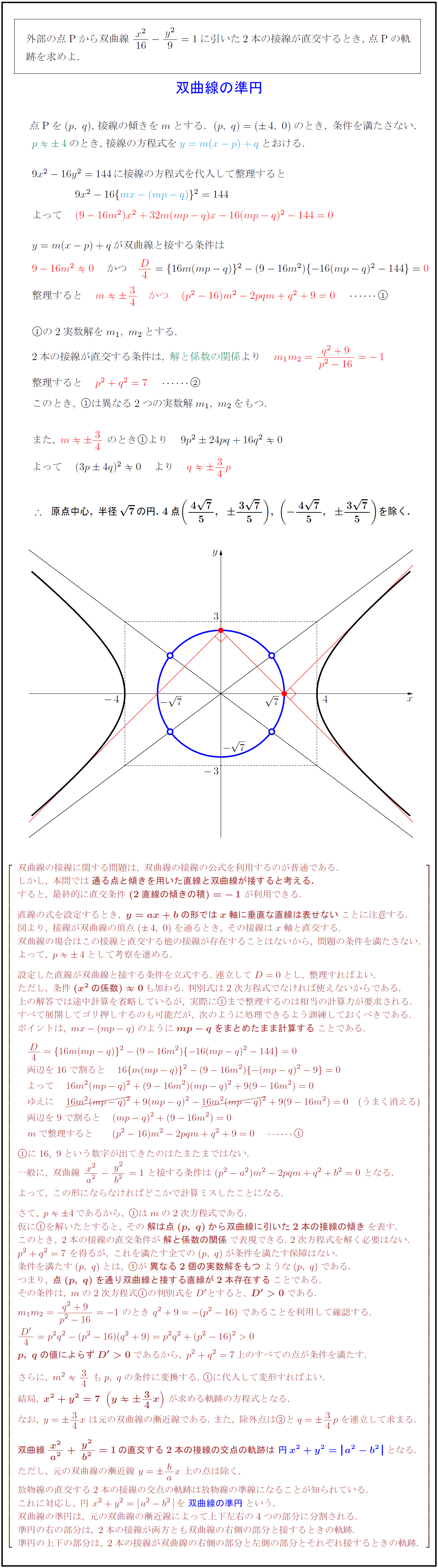



高校数学 双曲線の準円 直交する2本の接線の交点の軌跡 受験の月




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ



高校数学 数 動画 双曲線 の問題 19ch




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
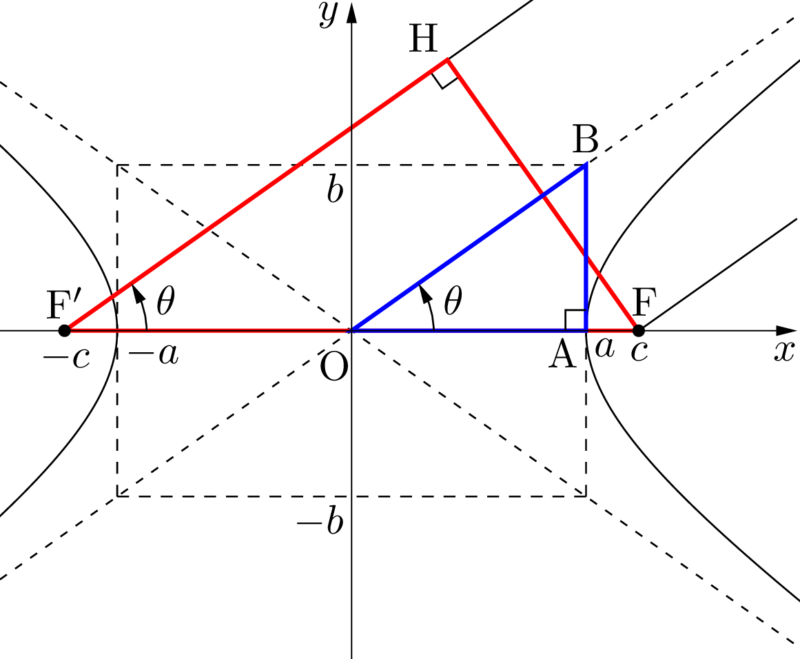



双曲線 焦点 媒介変数表示 極方程式 接線 群馬大 ページ 2 大学入試数学の考え方と解法




漸近線 の限界に漸近してみる Yoshidanobuo S Diaryー高校数学の 思考 判断 表現力 を磨こう ー
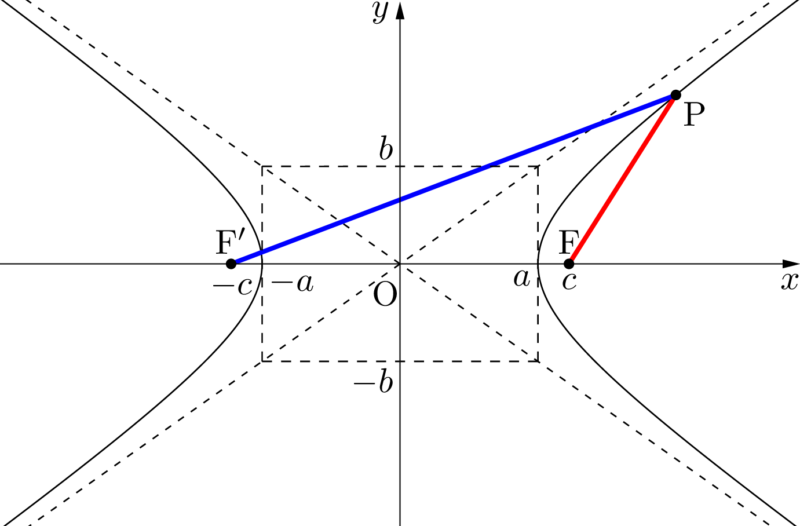



双曲線 焦点 媒介変数表示 極方程式 接線 群馬大 ページ 2 大学入試数学の考え方と解法



二次曲線




双曲線の漸近線の簡単な求め方と証明 高校数学の美しい物語




双曲線とは 例題と要点まとめでマスターしよう 高校生向け受験応援メディア 受験のミカタ
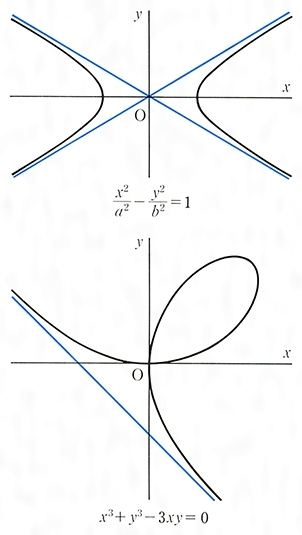



漸近線とは コトバンク
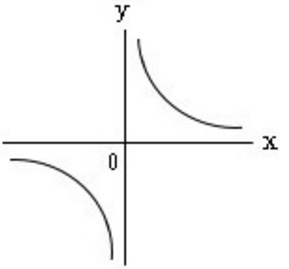



高校数学 分数関数のポイント整理 双曲線と漸近線 偏差値40プログラマー




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典
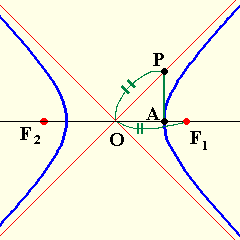



双曲線の基本性質




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ




数3の式と曲線についての質問です Clearnote
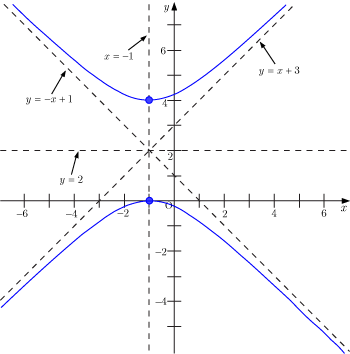



2次曲線に関する問題




二次曲線とは 双曲線の方程式の考え方と書き方 高校数学の知識庫
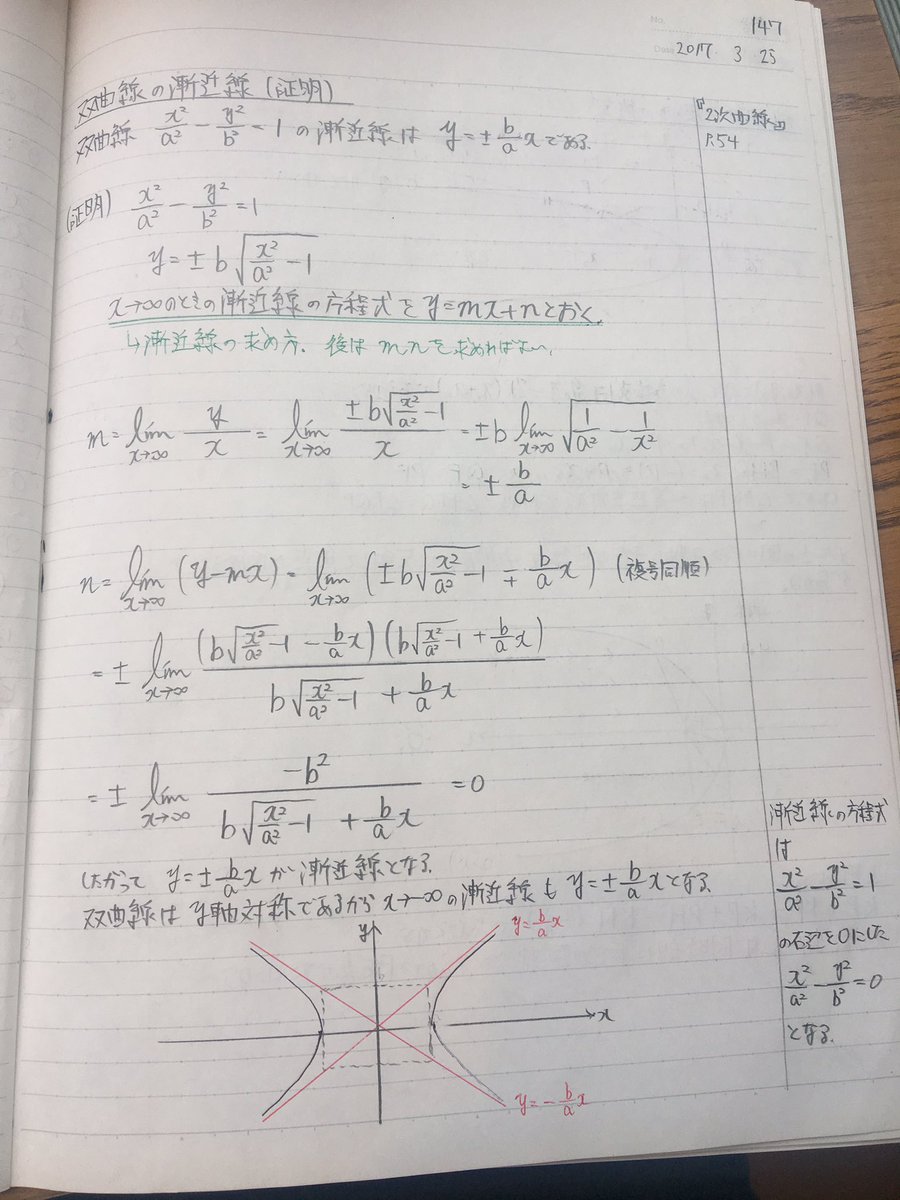



ゆな 双曲線の漸近線の証明 性質証明 2次曲線 双曲線 極限
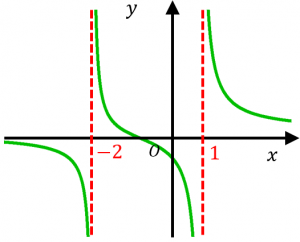



漸近線の求め方3パターン 具体例で学ぶ数学
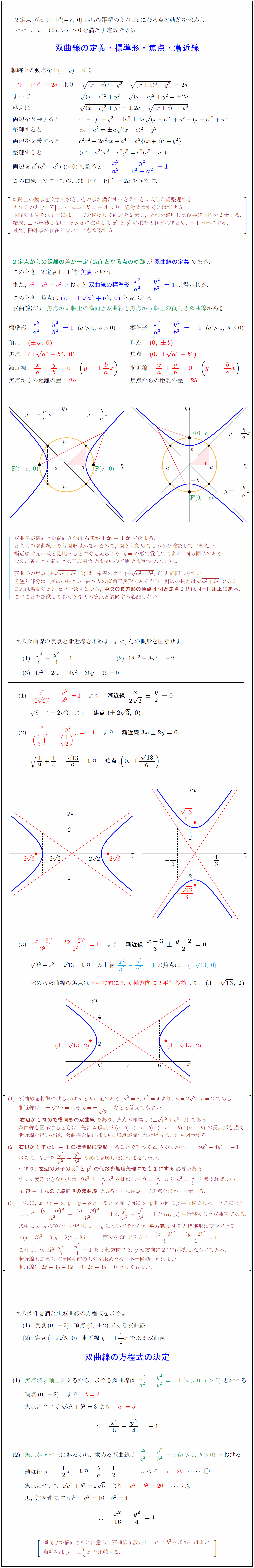



高校数学 双曲線の定義 標準形 焦点 漸近線 双曲線の方程式の決定 受験の月




標準 微分と関数のグラフと漸近線 なかけんの数学ノート




基本 双曲線と漸近線 なかけんの数学ノート



漸近線の求め方3パターン 具体例で学ぶ数学



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典




双曲線とは 式の導出とグラフ 漸近線までイラストでわかりやすく解説




定規だけで双曲線に接線を作図 定規とコンパスだけで双曲線の漸近線を作図 Mathlog
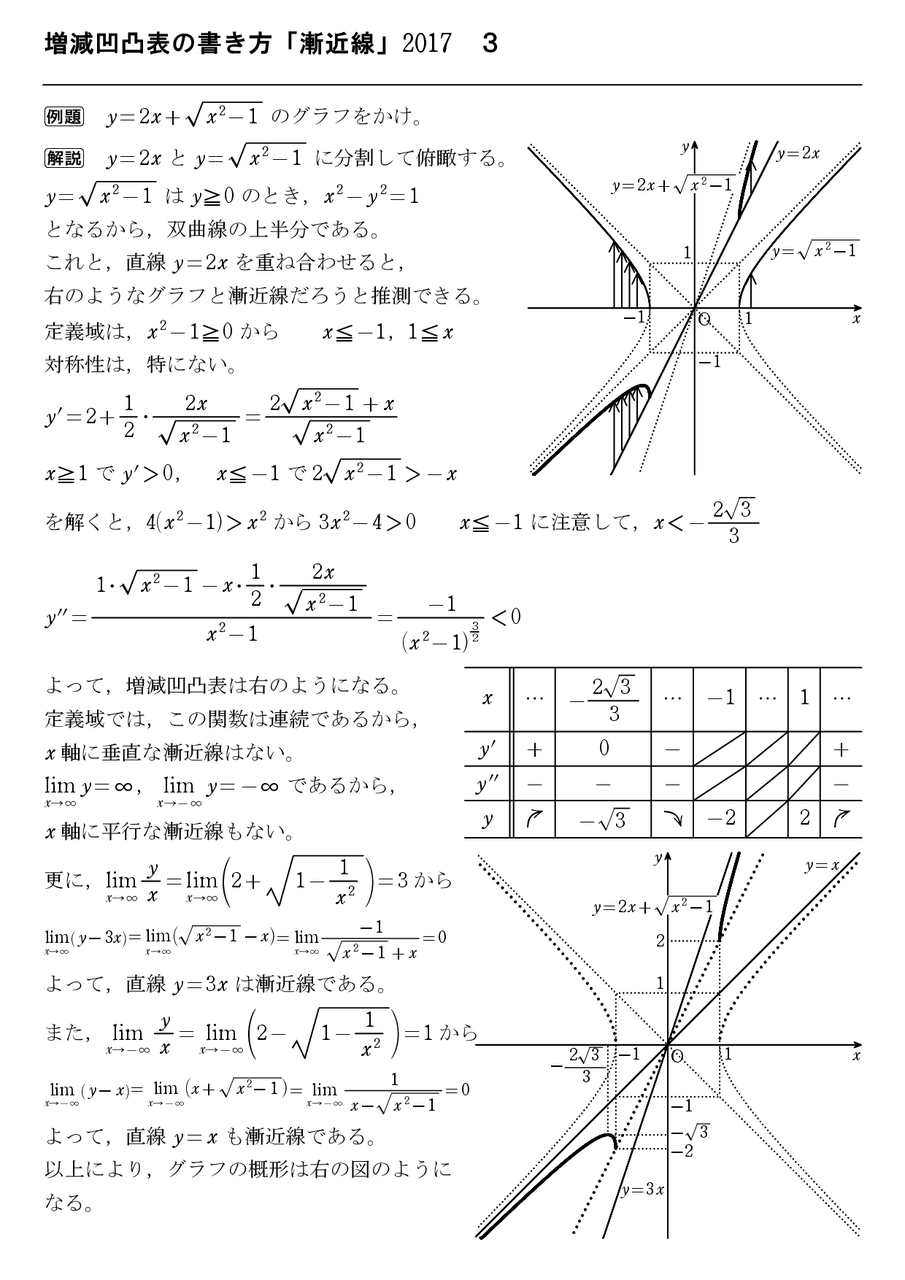



増減凹凸表の書き方 漸近線 17 3 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 2次曲線の決定 2 問題編 映像授業のtry It トライイット



1
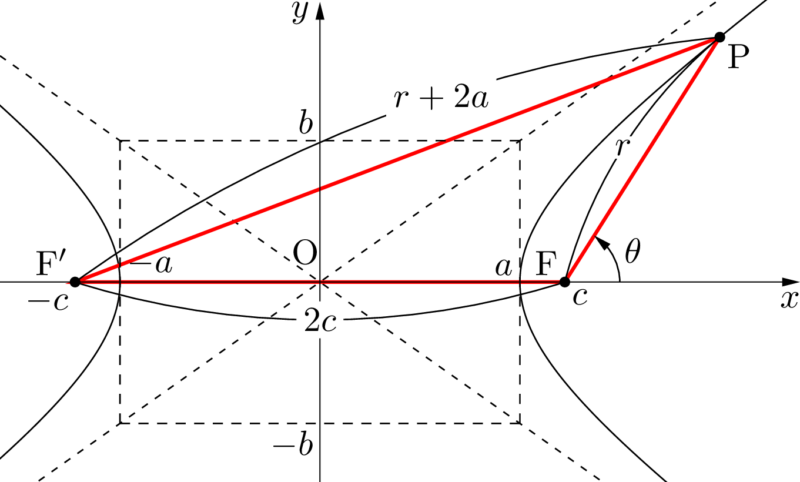



双曲線 焦点 媒介変数表示 極方程式 接線 群馬大 ページ 4 大学入試数学の考え方と解法
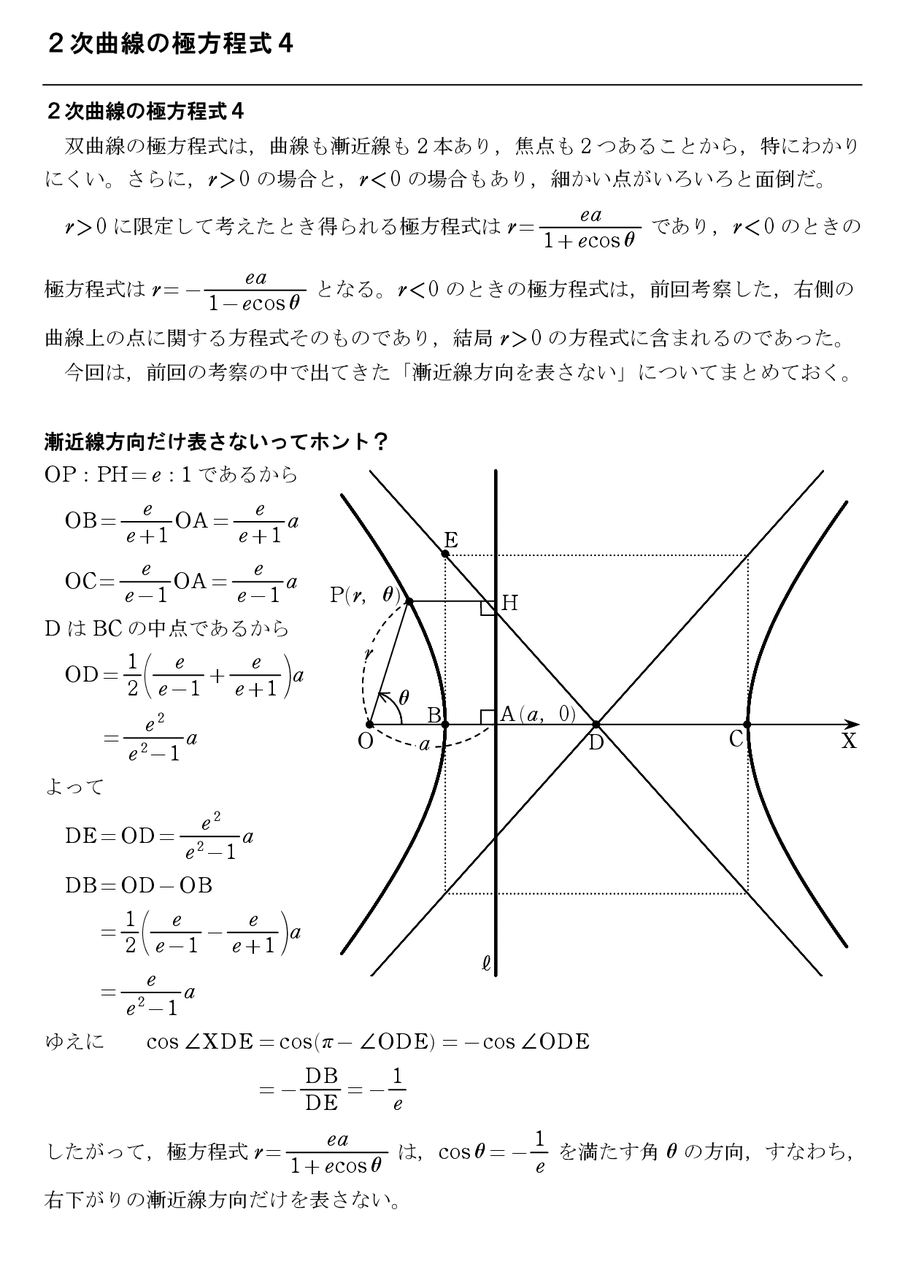



2次曲線の極方程式4 怜悧玲瓏 高校数学を天空から俯瞰する
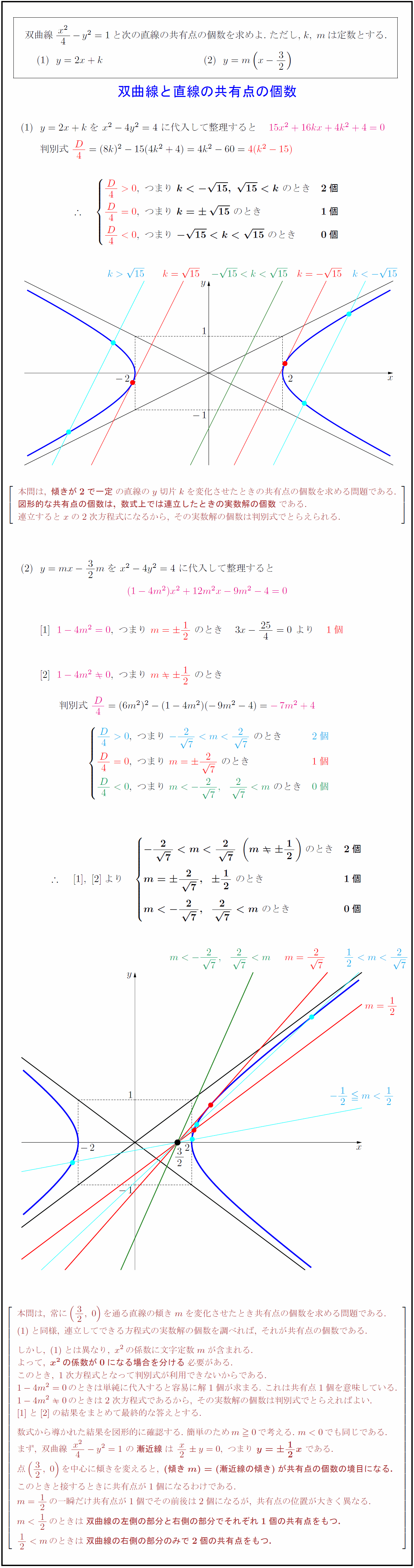



高校数学 双曲線と直線の共有点の個数 受験の月




双曲線の漸近線の簡単な求め方と証明 高校数学の美しい物語
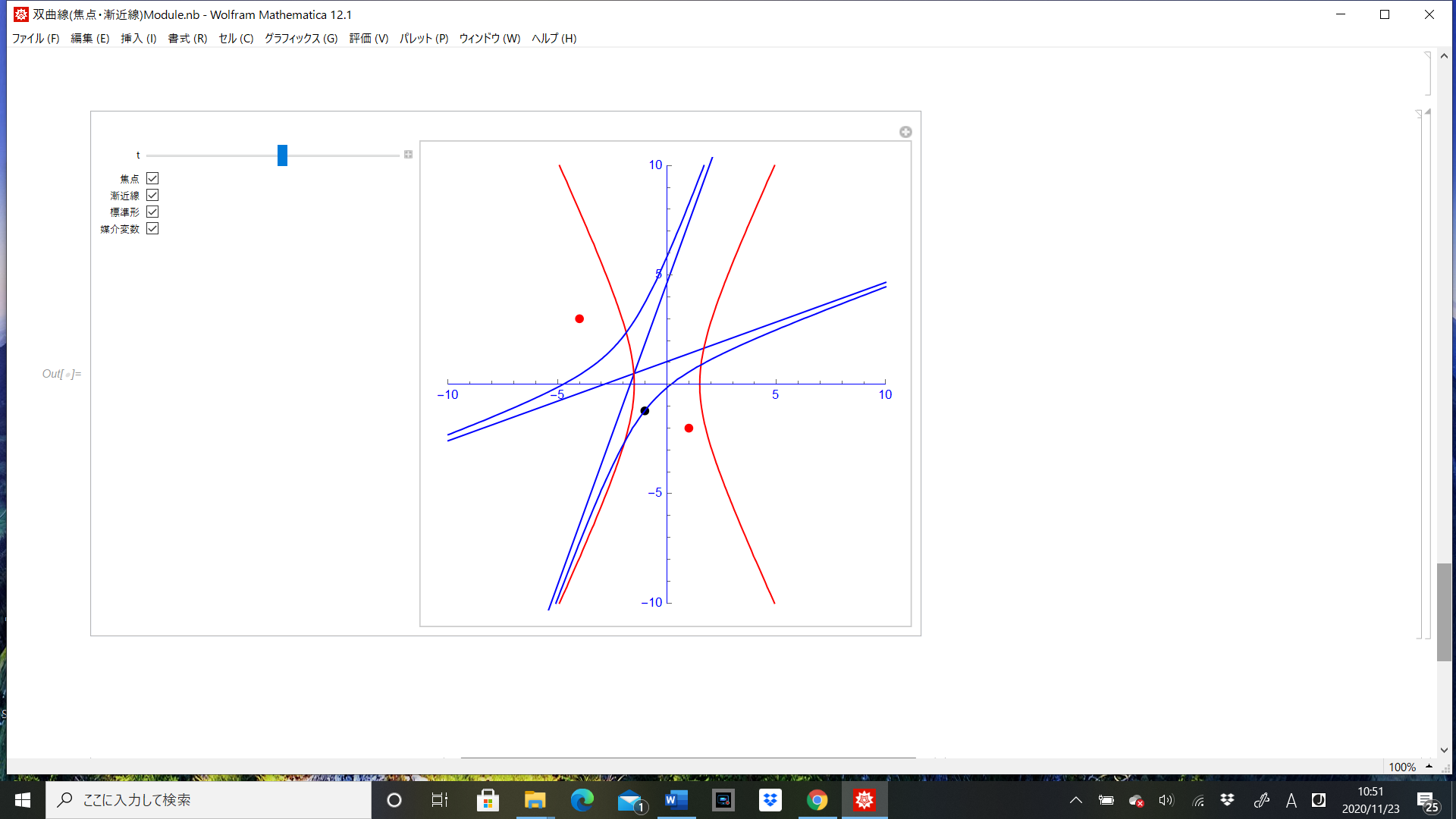



Mathematica Kobayashika64



双曲線の方程式




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ



双曲線 Wikipedia




定規だけで双曲線に接線を作図 定規とコンパスだけで双曲線の漸近線を作図 Mathlog




高校数学 双曲線のグラフ 1 映像授業のtry It トライイット



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典




数 微分法 漸近線 縦線タイプ オンライン無料塾 ターンナップ Youtube



双曲線x 2 A 2 Y 2 B 2 1上の点pから2つの漸近 Yahoo 知恵袋




二次曲線とは 双曲線の方程式の考え方と書き方 高校数学の知識庫




漸近線の方程式がy 2x 5 Y 2x 3で 点 1 1 を通る双曲線の方程式を その他 教育 科学 学問 教えて Goo




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



2



円錐曲線 数学 パースフリークス




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ



2
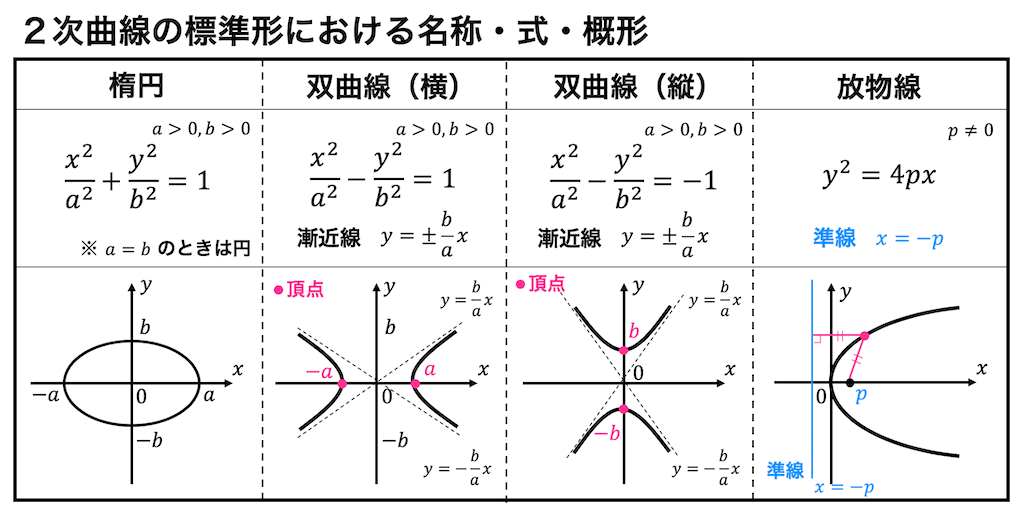



うさぎでもわかる線形代数 第21羽 2次形式の応用 2次曲線のグラフ 工業大学生ももやまのうさぎ塾



数3双曲線の漸近線の求め方で 最初にx A Y B 0とするのは何故で Yahoo 知恵袋




漸近線 Wikiwand
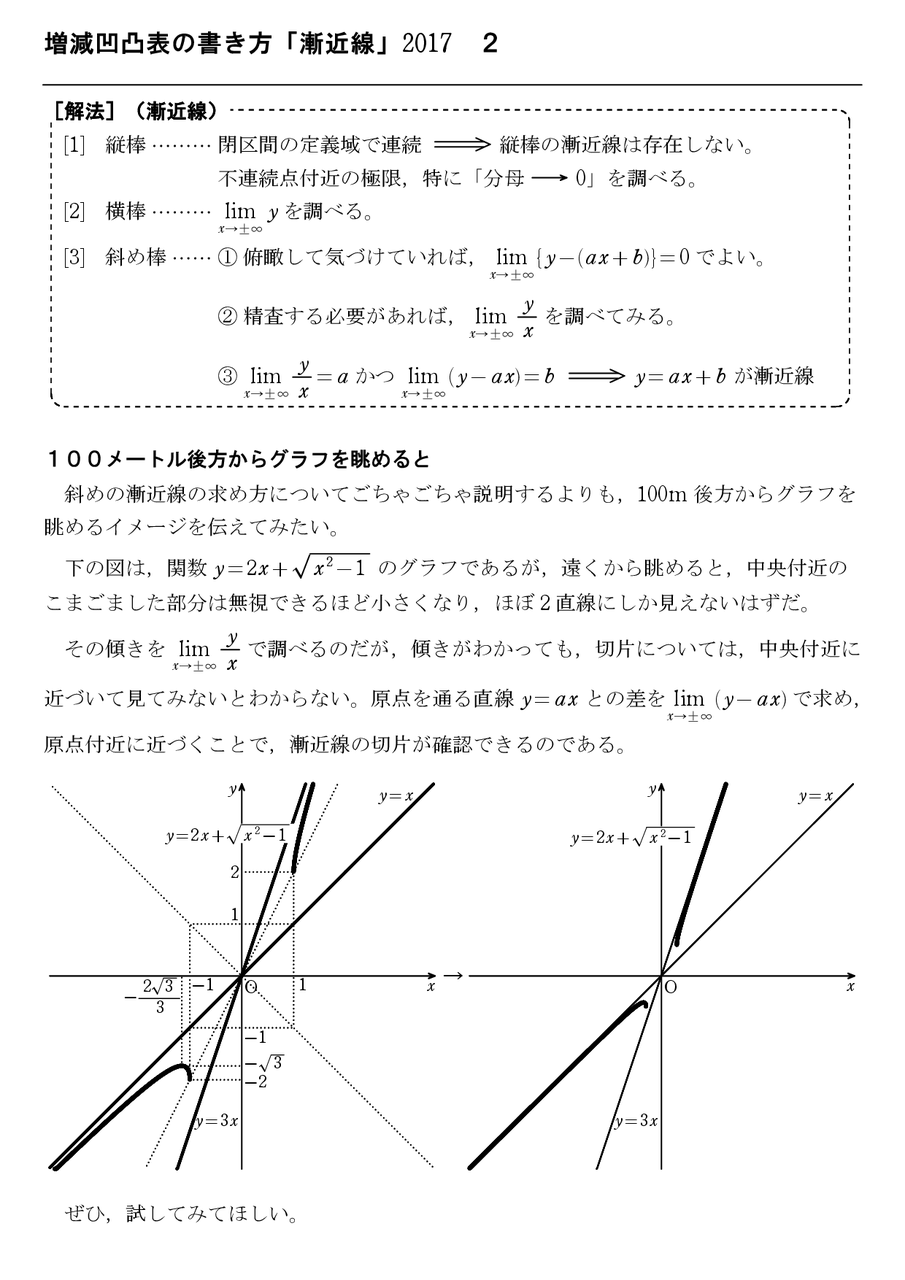



増減凹凸表の書き方 漸近線 17 2 怜悧玲瓏 高校数学を天空から俯瞰する




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




二つの漸近線から双曲線を求める方法 楕円では Okwave




高校数学 双曲線のグラフ 1 映像授業のtry It トライイット
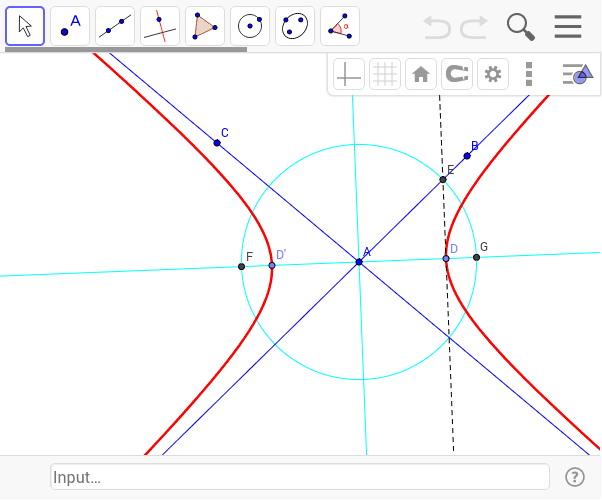



漸近線から双曲線を描く Geogebra
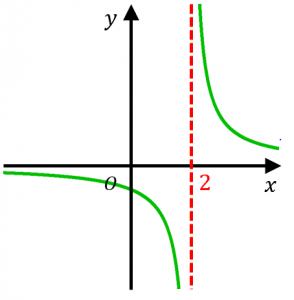



漸近線の求め方3パターン 具体例で学ぶ数学




高校数学 双曲線の接線と漸近線に関する有名性質 受験の月




双曲線です どうして B A がでてきて 2a となるのですか Clearnote
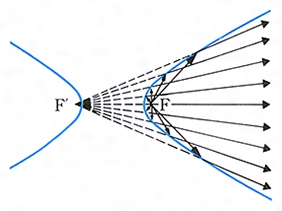



双曲線とは コトバンク




分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法




双曲線とは 例題と要点まとめでマスターしよう 高校生向け受験応援メディア 受験のミカタ




平面上の曲線 双曲線のグラフのかき方 数学 定期テスト対策サイト
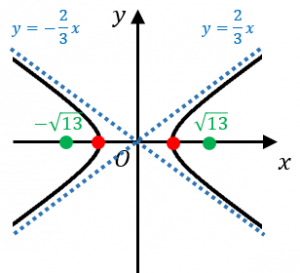



双曲線に関する公式まとめ 具体例で学ぶ数学




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



どうして 中心が原点 漸近線の傾きが 2で 点 1 2 0 を通 Yahoo 知恵袋



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典
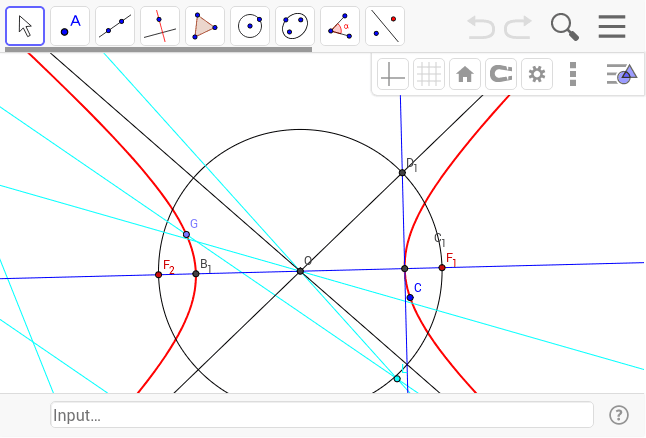



双曲線の焦点の求め方 Geogebra



双曲線 京極一樹の数学塾




数学 双曲線の標準形の読み取りと概形のコツ 教科書より詳しい高校数学
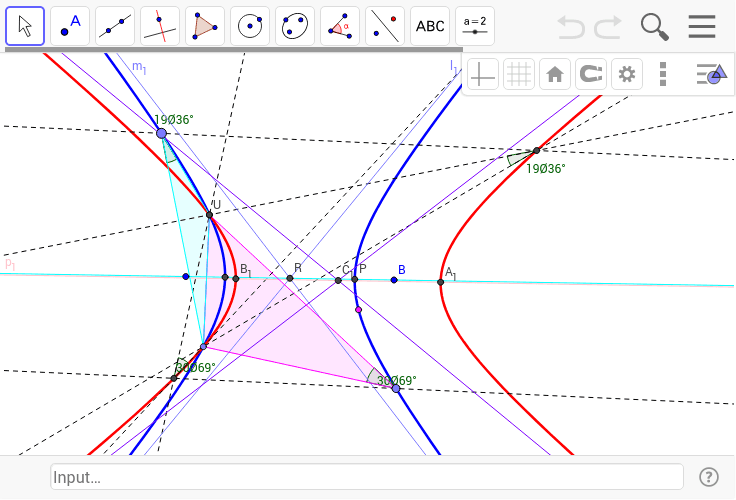



双子双曲線の漸近線は互いに直交する Geogebra




双曲線の焦点と漸近線 定義 高校数学 Youtube
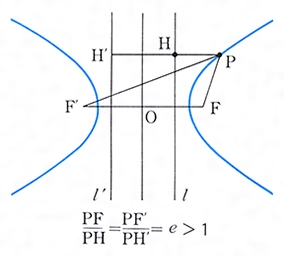



双曲線とは コトバンク




数学検定1級合格者が解説 双曲線の漸近線 焦点の覚え方つき 準1級 2回 1次 6 数検準1級 Youtube




数学iii 式と曲線 まなびの学園
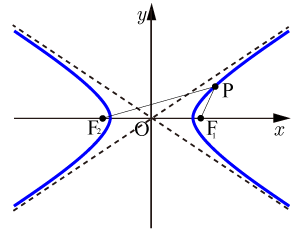



双曲線




高校数学 解答の 原点で交わる2つの漸近線をもち という記述がなぜ 数学 教えて Goo




双曲線とは 式の導出とグラフ 漸近線までイラストでわかりやすく解説



双曲線の焦点についての関係式 C 2 A 2 B 2 ほのぼの数学頑張ろう
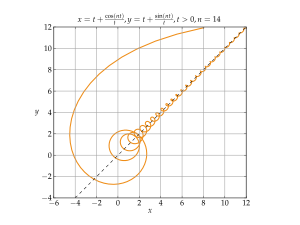



漸近線 Wikipedia




漸近線の求め方 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
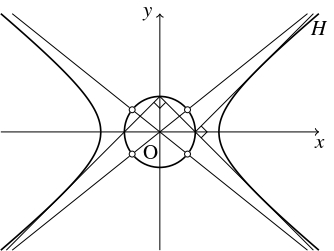



双曲線




定規だけで双曲線に接線を作図 定規とコンパスだけで双曲線の漸近線を作図 Mathlog



0 件のコメント:
コメントを投稿